Simplifying MBA Expressions to Solve a CTF

Last weekend my team and I competed in UofTCTF 2025, where we placed 9th overall. I found one of the reversing challenges really interesting, and I was proud of my solution and solve process, so I made a writeup for it.

Bloatware⌗

For this challenge we’re given a flag checker program, chal.js. Upon opening it I quickly saw that it was obfuscated with obfuscator.io and then minified. Here’s a small snippet of the code in question.

function _0x4d5c(){const _0x17b618=['Flag\x20is\x20in','split','from','stdout','Flag\x20is\x20co','length','Enter\x20the\x20','close','map','282sYzjLE','reduce','188pgfxnw','2868768dRvTVT','1096yWQTch','createInte','124052kiOzDS','15FeTOZN','question','charCodeAt','readline','3340895tLmyzT','correct!','every','flag:\x20','7177959hwqIPd','4632190uCcGWB','log','toString','rface','stdin','13629ChQgcp','rrect!'];_0x4d5c=function(){return _0x17b618;};return _0x4d5c();}const _0x42ff8b=_0x1461;(function(_0xbc9557,_0x3de0b9){const _0x4dbadc=_0x1461;const _0x3269ad=_0xbc9557();while(!![]){try{const _0x4adba0=parseInt(_0x4dbadc(0x10c))/0x1*(parseInt(_0x4dbadc(0x10e))/0x2)+-parseInt(_0x4dbadc(0x113))/0x3*(-parseInt(_0x4dbadc(0x112))/0x4)+parseInt(_0x4dbadc(0x117))/0x5+-parseInt(_0x4dbadc(0x10f))/0x6+-parseInt(_0x4dbadc(0x121))/0x7*(parseInt(_0x4dbadc(0x110))/0x8)+parseInt(_0x4dbadc(0x11b))/0x9+-parseInt(_0x4dbadc(0x11c))/0xa;if(_0x4adba0===_0x3de0b9){break;}else{_0x3269ad['push'](_0x3269ad['shift']());}}catch(_0x5166af){_0x3269ad['push'](_0x3269ad['shift']());}}}(_0x4d5c,0x6b3b1));

I did most of the deobfuscation by hand, because it was fairly straightforwards. I made a mistake in this step initially, but here is the correct deobfuscation.

const readline = require("readline");
const rl = readline.createInterface({
  'input': process.stdin,
  'output': process.stdout
});

let check_flag = function check_flag(_0x5bb3d9) {
  return check_flag = input => {
    input[input.length] = check_flag.toString().split('').map(c => c.charCodeAt(0x0)).reduce((a, b) => a + b, 0) ^ 0x27847c9d;
    if (input.length !== 0x79e) {
      return false;
    }
    conds = ["omitted for brevity"];
    return conds.every(a => a === true);
  };
}();

rl.question("Enter the flag: ", input => {
  const input_array = Array.from(input).map(c => c.charCodeAt(0));
  const result = check_flag(input_array);
  if (result) {
    console.log("Flag is correct!");
  } else {
    console.log("Flag is incorrect!");
  }
  rl.close();
});

The conds variable is a massive array of condition checks on the input that all look like this

0x1*(inp[0x184]&~inp[0x3c1])+0x1*inp[0x3c1]+-0x1*(inp[0x184]|inp[0x3c1]) == 0x0*~(inp[0x508]|inp[0x4f5])+-0x1*(~inp[0x508]|inp[0x4f5])

I removed most of the characters here because the full condition is too long and meaningless to include, but this is enough to get the idea. Each of the 1950 conditions are on the order of 2500 characters long, references 30+ elements of the input array, and evaluate to a boolean. This sort of equation, with both logical operations as well as normal arithmetic, is known as a mixed boolean-arithmetic (MBA) expression.

The program is effectively doing the following

1. Asks for the user to input the flag
2. Turns the input string into an array of integers based on each character’s ASCII code
3. Appends a new number to the array, found by summing the character values of the check_flag function as a string and then XORing with 0x27847c9d.
   • My first time looking at this I made a mistake in my deobfuscation and accidentally copied this operation as simply setting the last value to 0x27847c9d directly, skipping the string summation. I only realized this when a later step didn’t work
   • The function overwrites its own definition from inside itself, so it’s not possible to just print the value afterward. Additionally, it does this summation on the original string representation of the function, not the deobfuscated one (including the). The way to find the value was to copy the function out of the original minified code and run the .toString().split('').map(c => c.charCodeAt(0x0)).reduce((a, b) => a + b, 0) ^ 0x27847c9d on it as a string, which resulted in the value 431
4. Checks that the input was 1949 characters long
5. Iterates over 1950 conditions for the input array that all need to evaluate to true for it to return true, otherwise returns false
6. Prints the result of the flag check

Trying Z3⌗

After analyzing what the program does, it’s somewhat obvious that at its core, this challenge is about finding an array of numbers that fit a set of arbitrary constraints by solving it as a system of equations. This is a kind of problem that libraries such as Z3 are really good at. I learned about the existence of Z3 last year after writing my own constraint solver for the YARA challenge in Flare-On, only to learn afterward that tools for that already existed.

The first thing I tried was sticking a single constraint into Z3 to see if it could find a solution for it.

from z3 import *

INPUT_LEN = 1950

inp = [BitVec(f"input_{i}", 8) for i in range(INPUT_LEN)]

s = Solver()

with open("conds.js") as f:
    lines = f.readlines()

for l in lines[:1]:
    s.add(eval(l))

if s.check() == sat:
    m = s.model()
    result = [m[x] for x in m]
    print("solution found:")
    print(result)
else:
    print("no solution found")

There are a few problems here, most notably forgetting to set the last byte to 431, and also constraining the array values such that it couldn’t be 431. I made these mistakes because at this point in my solving process I hadn’t read the source code thoroughly enough, and as a result didn’t realize it was even hardcoding the final value (let alone know what it was setting it to). Despite these problems, this script did initially work as a proof of concept for Z3 solving these constraints. conds.js was a file I made with each of the condition checks on one line for easy parsing. When truncating the slice to only use a small number of the conditions, Z3 was very much able to find a valid solution vector (although obviously not the one I was looking for). However, when increasing the number of constraints used, the time it took Z3 to solve the system also increased dramatically. I measured how long it took for some small numbers of input constraints and graphed it on Desmos where x represents the number of constraints used, and y is the time in seconds it took to solve.

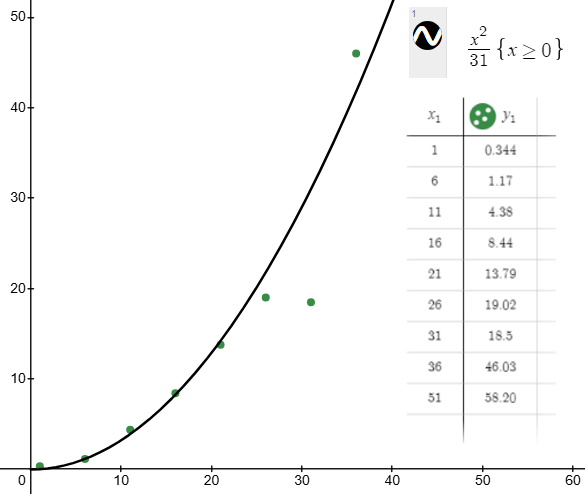
At least for small values, it seemed like for n input constraints, Z3 would solve the system in O(n^2) time. Some simple arithmetic would suggest that for 1950 input values it would take about 34 hours for my computer to solve it. While theoretically possible within the time of the CTF, this seemed very unlikely to be the proper solution, and I wanted to solve it without cheesing the solution.

After taking a minute to think about what I’d learned so far, I thought about what I knew to be true

1. The system is solvable in a sane amount of time, or else this wouldn’t be a reasonable challenge
2. Z3 is one of the most efficient tools that exist for solving these kinds of problems
3. There are 1950 constraints, each referencing 33 variables
4. The flag vector has 1950 elements, each presumably fitting within a single byte (not counting the final element which I still hadn’t remembered yet)
5. Each element is referenced by exactly 2 constraints, except for element 1950 which is referenced by all of them

Taking this information, I then made a few abductive inferences

1. Each of the constraints needs to simplify somehow, presumably in a way that results in referencing fewer variables per constraint
2. Given 1950 bytes (15600 bits) in the flag and 1950 constraints, each constraint needs to provide on average 8 bits of information
3. Z3’s inability to solve the problem quickly is a result of the equations not being simplified enough
4. In order to solve the problem I needed to simplify the constraint equations

Syntactic Approach to Simplification⌗

One of the first things I noticed when looking at the equations was that it contained a lot of nested parentheses, often multiplying entire groups by 0x0. No matter the value of these inner groups, they wouldn’t affect the overall result of the equation because of being multiplied by zero. There were also some other common easily simplifyable structures such as double negatives. A friend and I wrote a script that tried to reduce the complexity of the constraints by using regex to remove redundant components.

import re

with open("conds.js") as f:
    lines = f.readlines()

i = 0
for expr in lines[:1]:
    expr = re.sub(r'0x0\*\s*[~]?\([^)]*\)', '', expr)
    expr = re.sub(r'0x1\*', '', expr)
    expr = re.sub(r'-0x1\*', '-', expr)
    expr = re.sub(r'\+\+', '+', expr)
    expr = re.sub(r'\+-', '-', expr)
    expr = re.sub(r'~~', '', expr)
    expr = re.sub(r'--', '+', expr)

This method was successfully able to reduce the length of the equations by about 15% on average, but still nowhere near enough to make a difference.

The next potential solution I considered was inspired by another challenge I’d just finished - a pyjail that relied on the Python ast library to (try to) detect “dangerous code” before it was evaluated. That library (as the name implies) uses abstract syntax trees to represent the structure of a program, breaking it into a tree of nodes with parent-child relationships. I thought it could be an interesting idea to try using the same concept for parsing the mathematical expressions.

I considered a “node” to be a group contained by parentheses and identified by its child nodes and an operation being applied to it (which could either be a variable or a symbol). It was 3am at this point and I was feeling lazy so I explained my idea to an LLM to get a framework to build off of, and after tweaking it a lot to make it work I ended up with this code

class Node:
    def __init__(self, operation, children=None):
        self.operation = operation
        self.children = children if children else []
    def __repr__(self, level=0):
        indent = "  " * level
        result = f"{indent}Node(operation={self.operation}, children=[\n"
        for child in self.children:
            result += child.__repr__(level + 1)
        result += f"{indent}])\n"
        return result

    def is_leaf(self):
        return not self.children

def parse_expression(expression):
    stack = []
    current_node = Node(operation="root")
    stack.append(current_node)
    token = ""
    i = 0
    while i < len(expression):
        char = expression[i]
        if char == "(":
            if token.strip():
                stack[-1].children.append(Node(operation=token.strip()))
                token = ""
            new_node = Node(operation="group")
            stack[-1].children.append(new_node)
            stack.append(new_node)
        elif char == ")":
            if token.strip():
                stack[-1].children.append(Node(operation=token.strip()))
                token = ""
            stack.pop()
        elif char in "+-*/|&^~" and not (i + 1 < len(expression) and expression[i:i+2] == "**"):
            if token.strip():
                stack[-1].children.append(Node(operation=token.strip()))
                token = ""
            stack[-1].children.append(Node(operation=char))
        elif i + 1 < len(expression) and expression[i:i+2] == "**":
            if token.strip():
                stack[-1].children.append(Node(operation=token.strip()))
                token = ""
            stack[-1].children.append(Node(operation="**"))
            i += 1
        else:
            token += char
        i += 1
    if token.strip():
        stack[-1].children.append(Node(operation=token.strip()))
    return current_node

Again cutting out most of it for space reasons, this is the sort of output it produced when given one of the regex-parsed constraints as an input

Node(operation=group, children=[
    Node(operation=-, children=[])
    Node(operation=group, children=[
        Node(operation=inp[0x55], children=[])
        Node(operation=&, children=[])
        Node(operation=~, children=[])
        Node(operation=inp[0x42b], children=[
      ])
    ])
    Node(operation=+, children=[])
    Node(operation=group, children=[
        Node(operation=~, children=[])
        Node(operation=inp[0x55], children=[])
        Node(operation=&, children=[])
        Node(operation=inp[0x42b], children=[])
    ])
    Node(operation=-, children=[])
    Node(operation=inp[0x42b], children=[])
    Node(operation=+, children=[])
    Node(operation=inp[0x55], children=[])
])

This seemed really promising. My idea at this point was to write a way to give a node an arbitrary input array (values for all the inp variables) and have it compute the raw value of the node. Then, I would evaluate every node on a range of different inputs and identify the lowest-level nodes for which their values didn’t fluctuate depending on their inputs, and simplify them by replacing their contents with their true constant values. Doing this would let me identify and cut out all of the components that don’t actually affect the truthfulness of the expression, making it easier for Z3 to solve. For example, if I had the expression a - (( b * ~c + 5 ) ^ -( ~c * -b - 5)), it would be simplified to a because ( b * ~c + 5 ) ^ -( ~c * -b - 5) XORs two values that while variable, are always equivalent to each other thus resulting in 0. By evaluating with multiple different inputs I would in theory be able to identify nodes like this with a very small likelihood of a false positive.

I spent a while trying to implement the code to evaluate a node, but I ran into some issues likely posed by it being 4am by now and being incredibly tired. I had to wake up early to catch a flight the next day, so I made the decision to stop for the night and go to bed, and come back to the problem with a fresh pair of eyes the next day.

After waking back up I played around with my code a bit more, but kept running into the same roadblocks as before, so I ended up scrapping the idea. While waiting at the gate for my flight I had an idea for a method that would be a lot easier to implement, and I started working on it pretty much as soon as I got on the plane.

Just Guess⌗

One idea that I had in the back of my head for a while was that because each equation mathematically couldn’t be responsible for more than about 8 bits of information, each one on its own couldn’t really cut down on the space of valid solution vectors too much. It stood to reason that by making a random guess, while the odds of all of the conditions passing were next to zero, the odds of one of them passing was probably reasonably likely. Additionally, I considered the fact that if I was able to reduce the act of brute-forcing values from iterating over all possible values for all of the elements at once to iterating over them one element at a time, the problem would get a lot easier.

With this in mind, the first part of my idea for a new method of reducing the equations was to, for each of them

1. Brute-force input arrays until finding one that passes that specific condition
2. Iterate over the elements that are actually referenced in the equation, tweaking them one at a time and testing the condition again, saving a record of any that by being changed flip the output back to false

My code for this part looked like this

import random

conds = []
with open('conds.js') as f:
    for l in f.readlines():
        conds.append(l)
n = 0
expr = conds[n]
while True:
    inp = [random.randrange(0, 256) for i in range(1950)]
    check = (eval(expr))
    if(check):
        break
results = [[] for i in range(1950)]
saved_inp = inp[:]
for i in range(1950):
    if(hex(i) not in expr):
        continue
    for j in range(256):
        inp[i] = j
        check = (eval(expr))
        inp = saved_inp[:]
        if check:
            pass
        else:
            results[i].append(j)
            break
for i,j in enumerate(results):
    if len(j) > 0:
        print(i, saved_inp[i])

I started out by only testing on a single condition until I got the process down. As an aside, the conditions as-written in the challenge JS mean the same thing in Python syntax, which made it really easy to test by setting a local variable named inp and simply using Python’s eval function. Running this code gave me output I could work with.

1206 254
1572 225
1949 177

This meant that in a test in put that passed, the 1206th (0-indexed) value was 254, the 1572nd was 225, and the 1949th was 177. At this point I felt that I could probably assume that my methodology was mostly correct. Just knowing which indexes mattered and a set of values that worked obviously wouldn’t be enough on its own. The fact that it only took a couple thousand tries to guess a working array (when there are 16581375 permutations for those three bytes) meant that there had to be many values that worked, which meant I needed to properly find the pattern. To start figuring out the pattern I ran the program again to get a second set of working values

1206 218
1572 225
1949 213

Same three indexes, so clearly that part worked. I quickly noticed that both sets of numbers summed to 656, which stood out to me as probably important. I ran my script a few more times and confirmed that each of the sets of numbers it generated met the rule a + b + c = 656.

It stood to reason that the other conditions would behave similarly, but I wasn’t confident they would all reduce to the same simple addition, so I wrote the following function to test a suspected addition rule

def check_tri_sum(test):
    if len(test) != 4:
        return False
    for i in range(10):
        a = random.randrange(256)
        if test[3] - a < 300:
            b = 20
        else:
            b = random.randrange(256)
        c = test[3] - a - b
        inp = [0 for i in range(1950)]
        inp[test[0]], inp[test[1]] , inp[test[2]]  = a, b, c
        check = eval(expr, globals(), {'inp': inp})
        if not check:
            return False
    return True

This function takes an array of [a, b, c, sum] as an input, and validates that condition evaluates to true when a + b + c = sum by randomly generating 10 sets of values that meet the criteria and testing them. Obviously it’s possible for a false positive, but the odds are low enough that it doesn’t matter. After finding working values and testing if they met the summation rule or not I saved the results to a file like this.

if check_tri_sum(results):
    results.append("SUM")
    results.append(n)
    with open(f"./solves/solved_sum_{n}.txt", 'w') as f:
        f.write(str(results))
else:
    results = results[:-1]
    for j in [saved_inp[results[i]] for i in range(len(results))]:
        results.append(j)
    results.append("UNKNOWN")
    results.append(n)
    with open(f"./solves/unknown_{n}.txt", 'w') as f:
        f.write(str(results))

I did it this way by writing solutions to disk instead of just printing them as it found them because each one took enough time that I didn’t want to have to wait for them all to solve every time I executed my script. If the check_tri_sum function returned True it wrote a file that looked like this

[1206, 1572, 1949, 656, 'SUM', 0]

This meant that indexes 1206, 1572, and 1949 summed to 656, and that it was the 0th condition in the list. When check_tri_sum returned False instead, the output looked like this

[631, 1737, 1949, 246, 56, 243, 'UNKNOWN', 25]

Which told me that this was the 25th condition, and that the check passed when index 631 was 246, index 1737 was 56, and index 1949 was 243.

I let the script run for a while, and after about 10 minutes it had only gotten through about 30 or so values. This was really too slow, so I made a few optimizations.

results = []
saved_inp = inp[:]
for i in range(1950):
    if(hex(i) not in expr):
            continue
    for j in range(2):
        inp[i] = j
        check = eval(expr, globals(), {'inp': inp})
        inp = saved_inp[:]
        if not check:
            results.append(i)
            break

while True:
    i += 1
    inp = [random.randrange(0, 256) for i in range(1950)]
    check = eval(expr, globals(), {'inp': inp})
    if(check):
        break
    if i > 5000:
        broken = True
        break
if broken:
    print("skipping", n)
    continue

Firstly I changed the element iterator to only check 2 values per index instead of all 256, and second I capped the number of random guesses for a single condition at 5000, which was enough to filter out any of the harder ones to be dealt with later.

This performed faster, but still nowhere near fast enough. Luckily my laptop has a 16-thread CPU and this problem is incredibly suited to multiprocessing, so I modified my script a little further to run in 16 processes at once

import random
from multiprocessing import Process
import os
from typing import List

all_conds = []
skip = []
filenames = os.listdir("./solves")
nums_to_run = []

with open('conds.js') as f:
    for i,l in enumerate(f.readlines()):
        all_conds.append(l)
        if f"solved_sum_{i}.txt" not in filenames and f"unknown_{i}.txt" not in filenames:
            nums_to_run.append(i)
            pass
        else:
            skip.append(i)

def run_thread(cond_nums):
    for n in (cond_nums):
        ... # omitted

NUM_THREADS = 16
threads: List[Process] = []
for i in range(NUM_THREADS):
    threads.append(Process(target=run_thread, args=(nums_to_run[i::NUM_THREADS],)))

for t in threads:
    t.start()

for t in threads:
    t.join()

This worked MUCH faster, and it was able to work through the entire list of 1950 conditions in about half an hour. On the first try it found the simplified rule for about a third of the conditions, found a passing input but determined it wasn’t a summation rule for another third, and failed to find any working solutions within 5000 tries for the remaining third.

Before bumping up the max tries value and running the program again, I took a look at the solutions that I had marked as UNKNOWN. I played around with them a bit and noticed that for all of the ones I tried, they instead met the rule a + b - c = sum, which differs from the other rule in that one of the three values is subtracted rather than added. I wrote another function to test for this, and a script to convert all of the unknown_{n}.txt files into information I could use

import random
import os

filenames = os.listdir("./solves")
unknowns = [f for f in filenames if "unknown" in f]

all_conds = []
skip = []
nums_to_run = []

with open('conds.js') as f:
    for i,l in enumerate(f.readlines()):
        all_conds.append(l)

def run_thread(filenames):
    for f in (filenames):
        def sub_cond_check(v):
            if len(v) != 8:
                return None
            possible_diffs = [v[3]+v[4]-v[5], v[3]-v[4]+v[5], -v[3]+v[4]+v[5]]
            def rand_check_ordered(args):
                for i in range(10):
                    inp = [0 for i in range(1950)]
                    a = random.randrange(0, 256)
                    c = random.randrange(0, 16)
                    b = args[3] + c - a
                    inp[args[0]], inp[args[1]], inp[args[2]] = a, b, c
                    check = eval(expr, globals(), {'inp': inp})
                    if not check:
                        return False
                return True
            z = [v[0], v[1], v[2], possible_diffs[0]]
            if rand_check_ordered(z):
                return z
            z = [v[0], v[2],v[1], possible_diffs[1]]
            if rand_check_ordered(z):
                return z
            z = [ v[2],v[1],v[0], possible_diffs[2]]
            if rand_check_ordered(z):
                return z
            return None

        n = int(''.join([c for c in f if ord(c) >= ord('0') and ord(c) <= ord('9')]))
        expr = all_conds[n]
        if n in skip:
            continue

        with open(f"solves/{f}", 'r') as fo:
            fd = fo.read().strip()
        uk = eval(fd)
        checked = sub_cond_check(uk)
        checked.append("SUB_LAST")
        checked.append(n)
        print(checked)
        if (checked) is not None:
            with open(f"./solves/solved_sub_{n}.txt", 'w') as fo:
                fo.write(str(checked))
            os.remove(f"./solves/{f}")

run_thread(unknowns)

This was slightly more complicated than the addition check because I needed to test the case that each of the three variables was the negative one, but not really anything difficult. To my delight, all of the unknown values met this new rule, after which I was able to comfortably assume that there were only these two kinds of conditions.

I ran my original script a few more times, and after a certain point I stopped getting new solutions for summation rules. I realized that the subtraction rules were taking more guesses because there were fewer combinations of values that would result in them passing, so I changed my random array generation logic to accommodate to make it more likely. Nearly all of the values for these had two numbers on the upper end of 256 and one on the very low end, so I weighted the random variables as such.

def random_weighted_array():
    nums = [i for i in range(1950)]
    out = [0 for _ in range(1950)]
    for i in range(1950 // 3):
        j = random.choice(nums)
        nums.remove(j)
        out[j] = random.randrange(1, 16)
    for i in range(1950 - 1950 // 3):
        j = random.choice(nums)
        nums.remove(j)
        out[j] = random.randrange(230, 255)
    return out

This, along with bumping the max tries up to 100000, got me to 1946 out of 1950 conditions simplified. I changed my Z3 script a bit and tried again

from z3 import *
import os

n = 1950
bytes_ = [BitVec(f'byte_{i}', 8) for i in range(n)]
solver = Solver()

filenames = os.listdir("./solves")
for b in bytes_:
    solver.add(b >= 0, b <= 256)

for file in filenames:
    with open(f"./solves/{file}", 'r') as f:
        data = eval(f.read().strip())
    if "SUB_LAST" in data:
        solver.add(bytes_[data[0]] + bytes_[data[1]] - bytes_[data[2]] == data[3])
        pass
    elif "SUM" in data:
        solver.add(bytes_[data[0]] + bytes_[data[1]] + bytes_[data[2]] == data[3])

if solver.check() == sat:
    model = solver.model()
    for i in range(n):
        b = model[bytes_[i]]
        print((int(str(b))), end=',')
else:
    print("no solution found")

I was immediately met with no solution found, which was pretty disappointing. Clearly I was still doing something wrong. At this point I’d made it off my flight and back to my room and it was getting really late. After about half an hour of incoherent rants in my team’s chat about what I was doing and what wasn’t working, I finally made the realization that I’d neglected the fact that the final array value was supposed to be 431.

Considering that, it’s obvious why my script didn’t work - I was limiting the values of the solution vector to 256. I changed it to use 16 bit numbers instead of 8 bit numbers, and I was greeted with a working solution.

bytes_ = [BitVec(f'byte_{i}', 16) for i in range(n)]

I then added the constraint that bytes_[1949] == 431, and got the following output in about 5 seconds

117,111,102,116,99,116,102,123,98,49,48,52,116,119,52,114,51,95,98,49,55,119,105,122,51,95,52,110,100,95,51,118,52,49,95,49,122,95,115,48,95,115,49,109,112,108,51,95,98,117,55,95,122,51,95,49,53,95,55,48,48,95,115,108,48,119,95,50,95,115,48,108,118,51,95,108,109,52,48,95,117,110,108,51,122,122,95,121,48,117,95,115,49,109,112,108,49,102,121,95,116,104,48,122,51,95,77,66,65,122,95,98,101,99,52,117,122,51,95,116,104,51,114,51,95,97,114,51,95,106,117,53,55,95,116,48,48,95,109,52,110,121,95,118,52,114,49,52,98,108,51,122,95,88,68,68,68,68,68,68,68,95,110,48,119,95,116,49,109,101,95,102,48,114,95,97,95,98,117,78,99,72,95,48,102,95,98,51,52,117,116,49,102,117,49,95,49,121,114,49,99,53,95,119,51,0,114,51,95,110,48,95,53,55,114,52,110,54,51,114,53,95,55,48,95,108,48,118,51,95,121,48,117,95,107,110,48,119,95,55,104,51,95,114,117,108,51,53,95,52,110,100,95,53,48,95,100,48,95,49,95,52,95,102,117,108,108,95,99,48,109,109,49,55,109,51,110,55,39,53,95,119,104,52,55,95,49,160,52,109,95,55,104,49,110,107,49,110,54,95,48,102,95,121,48,117,95,119,48,117,108,100,110,39,55,95,54,51,55,95,55,104,49,53,95,102,114,48,109,95,52,110,121,95,48,55,104,51,114,95,54,117,121,95,49,95,106,117,53,55,95,119,52,110,110,52,95,55,51,108,108,95,121,48,117,95,104,48,119,95,49,39,52,109,95,102,51,51,108,49,110,54,95,54,48,55,55,52,95,109,52,107,51,95,121,48,117,95,117,110,100,51,114,53,55,52,110,100,95,110,51,118,51,114,95,54,48,110,110,52,95,54,49,118,51,95,121,48,117,95,117,112,95,110,51,118,51,114,95,54,48,110,110,52,95,108,51,55,95,121,48,117,95,100,48,119,110,95,110,51,118,51,114,95,54,48,110,110,52,95,114,117,110,95,52,114,48,117,110,100,95,52,110,100,95,100,51,53,51,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,109,52,107,51,95,121,48,117,95,99,114,121,95,110,51,118,51,114,95,54,48,110,110,52,95,53,52,121,95,54,48,48,100,98,121,51,95,110,51,118,51,114,95,54,48,110,110,52,95,55,51,108,108,95,52,95,108,49,51,95,52,110,100,95,104,117,114,55,95,121,48,117,95,119,51,39,118,51,95,107,110,48,119,110,95,51,52,99,104,95,48,55,104,51,114,95,102,48,114,95,53,48,95,108,48,110,54,95,121,48,117,114,95,104,51,52,114,55,39,53,95,98,51,51,110,95,52,99,104,49,110,54,44,95,98,117,55,95,121,48,117,39,114,51,95,55,48,48,95,53,104,121,95,55,48,95,53,52,0,95,49,55,95,49,110,53,49,100,51,44,95,119,51,95,98,48,55,104,95,107,110,48,119,95,119,104,52,55,39,53,95,98,51,51,110,95,54,48,49,110,54,95,48,110,95,119,51,95,107,110,48,119,95,55,104,51,95,54,52,109,51,95,52,110,100,95,119,51,39,114,51,95,54,48,110,110,52,95,112,108,52,121,95,49,55,95,52,110,100,95,49,102,95,121,48,117,95,52,53,107,95,109,51,95,104,48,119,95,49,39,52,109,95,102,51,51,108,49,110,54,95,100,48,110,39,55,95,55,51,108,108,95,109,51,95,121,48,117,39,114,51,95,55,48,48,95,98,108,49,110,100,95,55,48,95,53,51,51,95,110,51,118,51,114,95,54,48,110,110,52,95,54,49,118,51,95,121,48,117,95,117,112,95,110,51,118,51,114,95,54,48,110,110,52,95,108,51,55,95,121,48,117,95,100,48,119,110,95,110,51,118,51,114,95,54,48,110,110,52,95,114,117,110,95,52,114,48,117,110,100,95,52,110,100,95,100,51,53,51,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,109,52,107,51,95,121,48,117,95,99,114,121,95,110,51,118,51,114,95,54,48,110,110,52,95,53,52,121,95,54,48,48,100,98,121,51,95,110,51,118,51,114,95,54,48,110,110,52,95,55,51,108,108,95,52,95,108,49,51,95,52,110,100,95,104,117,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,54,49,118,51,95,121,48,117,95,117,112,95,110,51,118,51,114,95,54,48,110,110,52,95,108,51,55,95,121,48,117,95,100,48,119,110,95,110,51,118,51,114,95,54,48,110,110,52,95,114,117,110,95,52,114,48,117,110,100,95,52,110,100,95,100,51,53,51,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,109,52,107,51,95,121,48,117,95,99,114,121,95,110,51,118,51,114,95,54,48,110,110,52,95,53,52,121,95,54,48,48,100,98,121,51,95,110,51,118,51,114,95,54,48,110,110,52,95,55,51,108,108,95,52,95,108,49,51,95,52,110,100,95,104,117,114,55,95,121,48,117,95,119,51,39,118,51,95,107,110,48,119,110,95,51,52,99,104,95,48,55,104,51,114,95,102,48,114,95,53,48,95,108,48,110,54,95,121,48,117,114,95,104,51,52,114,55,39,53,95,98,51,51,110,95,52,99,104,49,110,54,44,95,98,117,55,95,121,48,117,39,114,51,95,55,48,48,95,53,104,121,95,55,48,95,53,52,121,95,49,55,95,49,110,53,49,100,51,44,95,119,51,95,98,48,55,104,95,107,110,48,119,95,119,104,52,55,39,53,95,98,51,51,110,95,54,48,49,110,54,95,48,110,95,119,51,95,107,110,48,119,95,55,104,51,95,54,52,109,51,95,52,110,100,95,119,51,39,114,51,95,54,48,110,110,52,95,112,108,52,121,95,49,55,95,49,95,106,117,53,55,95,119,52,110,110,52,95,55,51,108,108,95,121,48,117,95,104,48,119,95,49,39,52,109,95,102,51,51,108,49,110,54,95,54,48,55,55,52,95,109,52,107,51,95,121,48,117,95,117,110,100,51,114,53,55,52,110,100,95,110,51,118,51,114,95,54,48,110,110,52,95,54,49,118,51,95,121,48,117,95,117,112,95,110,51,118,51,114,95,54,48,110,110,52,95,108,51,55,95,121,48,117,95,100,48,119,110,95,110,51,118,51,114,95,54,48,110,110,52,95,114,117,110,95,52,114,48,117,110,100,95,52,110,100,95,100,51,53,51,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,109,52,107,51,95,121,48,117,95,99,114,121,95,110,51,118,51,114,95,54,48,110,110,52,95,53,52,121,95,54,48,48,100,98,121,51,95,110,51,118,51,114,95,54,48,110,110,52,95,55,51,108,108,95,52,95,108,49,51,95,52,110,100,95,104,117,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,54,49,118,51,95,121,48,117,95,117,112,95,110,51,118,51,114,95,54,48,110,110,52,95,108,51,55,95,84,48,117,95,100,48,119,110,95,110,51,118,51,114,95,54,48,110,110,52,95,114,117,110,95,52,114,48,117,110,100,95,52,110,100,95,100,51,53,51,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,109,52,107,51,95,121,48,117,95,99,114,121,95,110,51,118,51,114,95,54,48,110,110,52,95,53,52,121,95,54,48,48,100,98,121,51,95,110,51,118,51,114,95,54,48,110,110,52,95,55,51,108,108,95,52,95,108,49,51,95,52,110,100,95,104,117,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,54,49,118,51,95,121,48,117,95,117,112,95,110,51,118,51,114,95,54,48,110,110,52,95,108,51,55,95,121,48,117,95,100,48,119,110,95,110,51,118,51,114,95,54,48,110,110,52,95,114,117,110,95,52,114,48,117,110,100,95,52,110,100,95,100,51,53,51,114,55,95,121,48,117,95,110,51,118,51,114,95,54,48,110,110,52,95,109,52,107,51,95,121,48,117,95,99,114,121,95,110,51,118,51,114,95,54,48,110,110,52,95,53,52,121,95,54,48,48,100,98,121,51,95,110,51,118,51,114,95,54,48,110,110,52,95,55,51,108,108,95,52,95,108,49,51,95,52,110,100,95,104,117,114,55,95,121,48,117,95,119,48,119,95,121,48,117,95,114,51,52,49,49,121,95,100,49,100,95,49,55,63,70,125,431

Truncating the final dummy value and putting it into CyberChef, I decoded the bytes as ASCII and got this

This was really really close to the flag, but at least 3 (and I later figured out 4) of the values weren’t correct. I figured this was fairly obviously because of the 4 conditions I wasn’t able to simplify. I spent a minute trying to optimize my simplification script further given the known 1950th value, but before I got too far I realized that 4 is a very small number, and I could probably just throw the original, unaltered equations for those 4 into Z3 and it would take care of it for me. My final Z3 script looked like this (sans the constraints themselves which are still painfully long)

from z3 import *
import os

n = 1950
bytes_ = [BitVec(f'byte_{i}', 16) for i in range(n)]
solver = Solver()
filenames = os.listdir("./solves")

for b in bytes_:
    solver.add(b >= 0, b <= 1024)

solver.add(bytes_[1949] == 431)

for file in filenames:
    with open(f"./solves/{file}", 'r') as f:
        data = eval(f.read().strip())
    if "SUB_LAST" in data:
        solver.add(bytes_[data[0]] + bytes_[data[1]] - bytes_[data[2]] == data[3])
        pass
    elif "SUM" in data:
        solver.add(bytes_[data[0]] + bytes_[data[1]] + bytes_[data[2]] == data[3])

solver.add(-0x1*~(bytes_[0x106]|bytes_[0x3c])...)
solver.add(0x1*~bytes_[0x4ac]+-0x1*(~bytes_[0x4ac]|bytes_[0x584])...)
solver.add(0x0*(bytes_[0x4b8]|~bytes_[0x416])+-0x1*bytes_[0x4b8]...)
solver.add(0x1*(bytes_[0x2bc]|bytes_[0xb1])+-0x1*bytes_[0x2bc]...)

if solver.check() == sat:
    model = solver.model()
    for i in range(n):
        b = model[bytes_[i]]
        print(chr(int(str(b))), end='')
    print()
else:
    print("No solution found.")

Running this printed out the flag in its entirety

uoftctf{b104tw4r3_b17wiz3_4nd_3v41_1z_s0_s1mpl3_bu7_z3_15_700_sl0w_2_s0lv3_lm40_unl3zz_y0u_s1mpl1fy_th0z3_MBAz_bec4uz3_th3r3_ar3_ju57_t00_m4ny_v4r14bl3z_XDDDDDDD_n0w_t1me_f0r_a_buNcH_0f_b34ut1fu1_1yr1c5_w3'r3_n0_57r4n63r5_70_l0v3_y0u_kn0w_7h3_rul35_4nd_50_d0_1_4_full_c0mm17m3n7'5_wh47_1'4m_7h1nk1n6_0f_y0u_w0uldn'7_637_7h15_fr0m_4ny_07h3r_6uy_1_ju57_w4nn4_73ll_y0u_h0w_1'4m_f33l1n6_60774_m4k3_y0u_und3r574nd_n3v3r_60nn4_61v3_y0u_up_n3v3r_60nn4_l37_y0u_d0wn_n3v3r_60nn4_run_4r0und_4nd_d353r7_y0u_n3v3r_60nn4_m4k3_y0u_cry_n3v3r_60nn4_54y_600dby3_n3v3r_60nn4_73ll_4_l13_4nd_hur7_y0u_w3'v3_kn0wn_34ch_07h3r_f0r_50_l0n6_y0ur_h34r7'5_b33n_4ch1n6,_bu7_y0u'r3_700_5hy_70_54y_17_1n51d3,_w3_b07h_kn0w_wh47'5_b33n_601n6_0n_w3_kn0w_7h3_64m3_4nd_w3'r3_60nn4_pl4y_17_4nd_1f_y0u_45k_m3_h0w_1'4m_f33l1n6_d0n'7_73ll_m3_y0u'r3_700_bl1nd_70_533_n3v3r_60nn4_61v3_y0u_up_n3v3r_60nn4_l37_y0u_d0wn_n3v3r_60nn4_run_4r0und_4nd_d353r7_y0u_n3v3r_60nn4_m4k3_y0u_cry_n3v3r_60nn4_54y_600dby3_n3v3r_60nn4_73ll_4_l13_4nd_hur7_y0u_n3v3r_60nn4_61v3_y0u_up_n3v3r_60nn4_l37_y0u_d0wn_n3v3r_60nn4_run_4r0und_4nd_d353r7_y0u_n3v3r_60nn4_m4k3_y0u_cry_n3v3r_60nn4_54y_600dby3_n3v3r_60nn4_73ll_4_l13_4nd_hur7_y0u_w3'v3_kn0wn_34ch_07h3r_f0r_50_l0n6_y0ur_h34r7'5_b33n_4ch1n6,_bu7_y0u'r3_700_5hy_70_54y_17_1n51d3,_w3_b07h_kn0w_wh47'5_b33n_601n6_0n_w3_kn0w_7h3_64m3_4nd_w3'r3_60nn4_pl4y_17_1_ju57_w4nn4_73ll_y0u_h0w_1'4m_f33l1n6_60774_m4k3_y0u_und3r574nd_n3v3r_60nn4_61v3_y0u_up_n3v3r_60nn4_l37_y0u_d0wn_n3v3r_60nn4_run_4r0und_4nd_d353r7_y0u_n3v3r_60nn4_m4k3_y0u_cry_n3v3r_60nn4_54y_600dby3_n3v3r_60nn4_73ll_4_l13_4nd_hur7_y0u_n3v3r_60nn4_61v3_y0u_up_n3v3r_60nn4_l37_y0u_d0wn_n3v3r_60nn4_run_4r0und_4nd_d353r7_y0u_n3v3r_60nn4_m4k3_y0u_cry_n3v3r_60nn4_54y_600dby3_n3v3r_60nn4_73ll_4_l13_4nd_hur7_y0u_n3v3r_60nn4_61v3_y0u_up_n3v3r_60nn4_l37_y0u_d0wn_n3v3r_60nn4_run_4r0und_4nd_d353r7_y0u_n3v3r_60nn4_m4k3_y0u_cry_n3v3r_60nn4_54y_600dby3_n3v3r_60nn4_73ll_4_l13_4nd_hur7_y0u_w0w_y0u_r3411y_d1d_17?!}

After having solved the challenge I spoke to the challenge author about my solution, and I was informed that there already existed a tool to do exactly what I’d spent the last day painstakingly figuring out on my own (which was painfully reminiscent of learning about Z3 only after solving the Flare-On challenge on my own 😭).

Despite this, I probably learned quite a bit more from struggling through this challenge the hard way and doing it on my own, and I had fun solving it. My final simplification script is here, along with the original chal.js and the extracted constraints